Redis HyperLogLog和事务及7.0新特性
Redis高级数据结构HyperLogLog
HyperLogLog(Hyper[ˈhaɪpə(r)])并不是一种新的数据结构(实际类型为字符串类型),而是一种基数算法,通过HyperLogLog可以利用极小的内存空间完成独立总数的统计,数据集可以是IP、Email、ID等。
如果你负责开发维护一个大型的网站,有一天产品经理要网站每个网页每天的 UV 数据,然后让你来开发这个统计模块,你会如何实现?
如果统计 PV 那非常好办,给每个网页一个独立的 Redis 计数器就可以了,这个计数器的 key 后缀加上当天的日期。这样来一个请求,incrby 一次,最终就可以统计出所有的 PV 数据。
但是 UV 不一样,它要去重,同一个用户一天之内的多次访问请求只能计数一次。这就要求每一个网页请求都需要带上用户的 ID,无论是登陆用户还是未登陆用户都需要一个唯一 ID 来标识。
一个简单的方案,那就是为每一个页面一个独立的 set 集合来存储所有当天访问过此页面的用户 ID。当一个请求过来时,我们使用 sadd 将用户 ID 塞进去就可以了。通过 scard 可以取出这个集合的大小,这个数字就是这个页面的 UV 数据。
但是,如果你的页面访问量非常大,比如一个爆款页面几千万的 UV,你需要一个很大的 set 集合来统计,这就非常浪费空间。如果这样的页面很多,那所需要的存储空间是惊人的。为这样一个去重功能就耗费这样多的存储空间,值得么?其实需要的数据又不需要太精确,1050w 和 1060w 这两个数字对于老板们来说并没有多大区别,So,有没有更好的解决方案呢?
这就是HyperLogLog 的用武之地,Redis 提供了 HyperLogLog 数据结构就是用来解决这种统计问题的。HyperLogLog 提供不精确的去重计数方案,虽然不精确但是也不是非常不精确,Redis官方给出标准误差是 0.81%,这样的精确度已经可以满足上面的 UV 统计需求了。
操作命令
HyperLogLog提供了3个命令: pfadd、pfcount、pfmerge。
例如08-15的访问用户是u1、u2、u3、u4,08-16的访问用户是u-4、u-5、u-6、u-7
pfadd
pfadd key element [element …]
pfadd用于向HyperLogLog 添加元素,如果添加成功返回1:
pfadd 08-15:u:id “u1” “u2” “u3” “u4”
pfcount
pfcount key [key …]
pfcount用于计算一个或多个HyperLogLog的独立总数,例如08-15:u:id的独立总数为4:
pfcount 08-15:u:id
如果此时向插入u1、u2、u3、u90,结果是5:
pfadd 08-15:u:id “u1” “u2” “u3” “u90”
pfcount 08-15:u:id
如果我们继续往里面插入数据,比如插入100万条用户记录。内存增加非常少,但是pfcount 的统计结果会出现误差。
以使用集合类型和 HperLogLog统计百万级用户访问次数的占用空间对比:
数据类型 1天 1个月 1年
集合类型 80M 2.4G 28G
HyperLogLog 15k 450k 5M
可以看到,HyperLogLog内存占用量小得惊人,但是用如此小空间来估算如此巨大的数据,必然不是100%的正确,其中一定存在误差率。前面说过,Redis官方给出的数字是0.81%的失误率。
pfmerge
pfmerge destkey sourcekey [sourcekey … ]
pfmerge可以求出多个HyperLogLog的并集并赋值给destkey,请自行测试。
原理概述
基本原理
HyperLogLog基于概率论中伯努利试验并结合了极大似然估算方法,并做了分桶优化。
实际上目前还没有发现更好的在大数据场景中准确计算基数的高效算法,因此在不追求绝对准确的情况下,使用概率算法算是一个不错的解决方案。概率算法不直接存储数据集合本身,通过一定的概率统计方法预估值,这种方法可以大大节省内存,同时保证误差控制在一定范围内。目前用于基数计数的概率算法包括:
Linear Counting(LC):早期的基数估计算法,LC在空间复杂度方面并不算优秀;
LogLog Counting(LLC):LogLog Counting相比于LC更加节省内存,空间复杂度更低;
HyperLogLog Counting(HLL):HyperLogLog Counting是基于LLC的优化和改进,在同样空间复杂度情况下,能够比LLC的基数估计误差更小。
举个例子来理解HyperLogLog 算法,有一天Fox老师和Mark老师玩抛硬币的游戏,规则是Mark老师负责抛硬币,每次抛的硬币可能正面,可能反面,每当抛到正面为一回合,Mark老师可以自己决定进行几个回合。最后需要告诉Fox老师最长的那个回合抛了多少次以后出现了正面,再由Fox老师来猜Mark老师一共进行了几个回合。
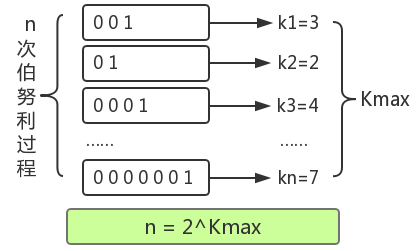
进行了n次,比如上图:
第一次: 抛了3次才出现正面,此时 k=3,n=1
第二次试验: 抛了2次才出现正面,此时 k=2,n=2
第三次试验: 抛了4次才出现正面,此时 k=4,n=3
…………
第n 次试验:抛了7次才出现正面,此时我们估算,k=7,n=n
k是每回合抛到1(硬币的正面)所用的次数,我们已知的是最大的k值,也就是Mark老师告诉Fox老师的数,可以用k_max表示。由于每次抛硬币的结果只有0和1两种情况,因此,能够推测出k_max在任意回合出现的概率 ,并由kmax结合极大似然估算的方法推测出n的次数n = 2^(k_max) 。概率学把这种问题叫做伯努利实验。
现在Mark老师已经完成了n个回合,并且告诉Fox老师最长的一次抛了4次,Fox老师此时也胸有成竹,马上说出他的答案16,最后的结果是:Mark老师只抛了3回合,
这三个回合中k_max=4,放到公式中,Fox老师算出n=2^4,于是推测Mark老师抛了16个回合,但是Fox老师输了,要负责买奶茶一个星期。
所以这种预估方法存在较大误差,为了改善误差情况,HLL中引入分桶平均的概念。
同样举抛硬币的例子,如果只有一组抛硬币实验,显然根据公式推导得到的实验次数的估计误差较大;如果100个组同时进行抛硬币实验,样本数变大,受运气影响的概率就很低了,每组分别进行多次抛硬币实验,并上报各自实验过程中抛到正面的抛掷次数的最大值,就能根据100组的平均值预估整体的实验次数了。
分桶平均的基本原理是将统计数据划分为m个桶,每个桶分别统计各自的k_max, 并能得到各自的基数预估值,最终对这些基数预估值求平均得到整体的基数估计值。LLC中使用几何平均数预估整体的基数值,但是当统计数据量较小时误差较大;HLL在LLC基础上做了改进,采用调和平均数过滤掉不健康的统计值。
什么叫调和平均数呢?举个例子
求平均工资:A的是1000/月,B的30000/月。采用平均数的方式就是: (1000 + 30000) / 2 = 15500
采用调和平均数的方式就是: 2/(1/1000 + 1/30000) ≈ 1935.484
可见调和平均数比平均数的好处就是不容易受到大的数值的影响,比平均数的效果是要更好的。
结合实例理解原理
现在我们和前面的业务场景进行挂钩:统计网页每天的 UV 数据。
1.转为比特串
通过hash函数,将数据转为比特串,例如输入5,便转为:101,字符串也是一样。为什么要这样转化呢?
是因为要和抛硬币对应上,比特串中,0 代表了反面,1 代表了正面,如果一个数据最终被转化了 10010000,那么从右往左,从低位往高位看,我们可以认为,首次出现 1 的时候,就是正面。
那么基于上面的估算结论,我们可以通过多次抛硬币实验的最大抛到正面的次数来预估总共进行了多少次实验,同样也就可以根据存入数据中,转化后的出现了 1 的最大的位置 k_max 来估算存入了多少数据。
2.分桶
分桶就是分多少轮。抽象到计算机存储中去,存储的是一个长度为 L 的位(bit)大数组 S ,将 S 平均分为 m 组,这个 m 组,就是对应多少轮,然后每组所占有的比特个数是平均的,设为 P。容易得出下面的关系:
L = S.length
L = m * p
以 K 为单位,S 占用的内存 = L / 8 / 1024
3、对应
假设访问用户 id 为:idn , n->0,1,2,3….
在这个统计问题中,不同的用户 id 标识了一个用户,那么我们可以把用户的 id 作为被hash的输入。即:
hash(id) = 比特串
不同的用户 id,拥有不同的比特串。每一个比特串,也必然会至少出现一次 1 的位置。我们类比每一个比特串为一次伯努利试验。
现在要分轮,也就是分桶。所以我们可以设定,每个比特串的前多少位转为10进制后,其值就对应于所在桶的标号。假设比特串的低两位用来计算桶下标志,总共有4个桶,此时有一个用户的id的比特串是:1001011000011。它的所在桶下标为:12^1 + 12^0 = 3,处于第3个桶,即第3轮中。
上面例子中,计算出桶号后,剩下的比特串是:10010110000,从低位到高位看,第一次出现 1 的位置是 5 。也就是说,此时第3个桶中,k_max = 5。5 对应的二进制是:101,将 101 存入第3个桶。
模仿上面的流程,多个不同的用户 id,就被分散到不同的桶中去了,且每个桶有其 k_max。然后当要统计出某个页面有多少用户点击量的时候,就是一次估算。最终结合所有桶中的 k_max,代入估算公式,便能得出估算值。
Redis 中的 HyperLogLog 实现
Redis的实现中,HyperLogLog 占据12KB(占用内存为=16834 * 6 / 8 / 1024 = 12K)的大小,共设有 16384 个桶,即:2^14 = 16384,每个桶有 6 位,每个桶可以表达的最大数字是:25+24+…+1 = 63 ,二进制为: 111 111 。
对于命令:pfadd key value
在存入时,value 会被 hash 成 64 位,即 64 bit 的比特字符串,前 14 位用来分桶,剩下50位用来记录第一个1出现的位置。
之所以选 14位 来表达桶编号是因为分了 16384 个桶,而 2^14 = 16384,刚好地,最大的时候可以把桶利用完,不造成浪费。假设一个字符串的前 14 位是:00 0000 0000 0010 (从右往左看) ,其十进制值为 2。那么 value 对应转化后的值放到编号为 2 的桶。
index 的转化规则:
首先因为完整的 value 比特字符串是 64 位形式,减去 14 后,剩下 50 位,假设极端情况,出现 1 的位置,是在第 50 位,即位置是 50。此时 index = 50。此时先将 index 转为 2 进制,它是:110010 。
因为16384 个桶中,每个桶是 6 bit 组成的。于是 110010 就被设置到了第 2 号桶中去了。请注意,50 已经是最坏的情况,且它都被容纳进去了。那么其他的不用想也肯定能被容纳进去。
因为 fpadd 的 key 可以设置多个 value。例如下面的例子:
pfadd lgh golang
pfadd lgh python
pfadd lgh java
根据上面的做法,不同的 value,会被设置到不同桶中去,如果出现了在同一个桶的,即前 14 位值是一样的,但是后面出现 1 的位置不一样。那么比较原来的 index 是否比新 index 大。是,则替换。否,则不变。
最终地,一个 key 所对应的 16384 个桶都设置了很多的 value 了,每个桶有一个k_max。此时调用 pfcount 时,按照调和平均数进行估算,同时加以偏差修正,便可以计算出 key 的设置了多少次 value,也就是统计值,具体的估算公式如下:
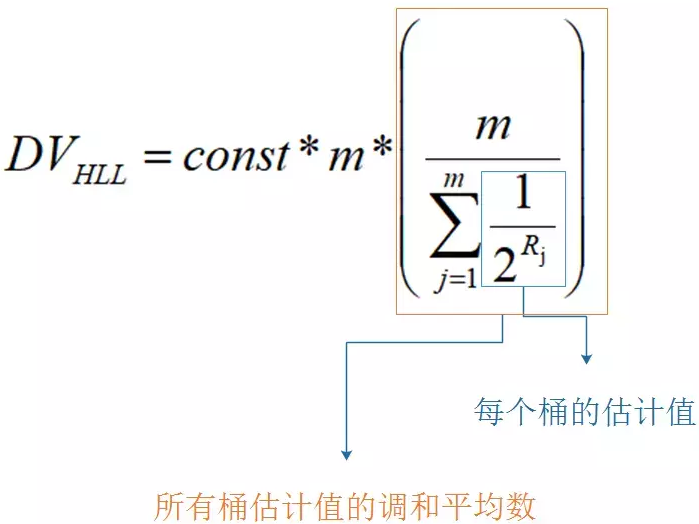
value 被转为 64 位的比特串,最终被按照上面的做法记录到每个桶中去。64 位转为十进制就是:2^64,HyperLogLog 仅用了:16384 * 6 /8 / 1024 =12K 存储空间就能统计多达 2^64 个数。
同时,在具体的算法实现上,HLL还有一个分阶段偏差修正算法。我们就不做更深入的了解了。
Redis事务
事务可以保证原子性,事务表示一组动作,要么全部执行,要么全部不执行。
例一:在微博上,A 关注了B,A的关注表就得有B的记录,而B的粉丝表列表得有A的记录。
例二:典型的银行转账,A给B转钱,A转出500,B收到后增加500。如果A转出500后 出现了错误,那么B是不可以增加500的,这两个行为要么全部执行,要么全部不执行,否则会出现数据不一致的情况。
事务命令
Redis提供了简单的事务功能,将一组需要一起执行的命令放到multi和exec两个命令之间。multi命令代表事务开始,exec命令代表事务结束,如果要停止事务的执行,可以使用discard命令代替exec命令即可。
1 | // 进入事务 |

值得注意的是,当我们通过multi命令开启事务后,执行了set命令后返回的queued,代表命令没有真正执行,而是存入到了redis的一个队列中,只有当我们执行了exec命令,redis才会真正的去执行 队列中存储的所有命令。
事务失效
redis的事务回滚分为2个情况,如果是命令上出现了错误,是会回滚的,如果是运行的时候出了错误,则不会回滚。
命令错误
我们故意把set写成sett,属于语法错误,这样事务会进行回滚。
1 | 127.0.0.1:1>multi |
运行错误
指:语法上没有错误,但是redis运行的时候出错了,这种 redis是不会进行事务回滚的。
下面我们用有序集合的add命令 为 set 无序集合添加元素,所以运行的过程肯定会出错。
1 | // 查询set集合中所有元素,可以看到元素是空的 |

watch(乐观锁)
有些应用场景需要在事务之前,确保事务中的key没有被其他客户端修改过,才执行事务,否则不执行(类似乐观锁)。
redis事务中提供了一个命令 watch 来实现类似于MySQL中的乐观锁。
A客户端创建Key并通过watch锁定
1 | // set 一个key值 ,value为666 |

如上所示,我们已经通过watch锁定了该值,锁定的值是666,我们开启事务后想去修改这个key的话,会先判断 key是否被人修改过了(判断value是否还是666),如果修改过了,事务就不会执行。
其他客户端修改这个key的值
1 | // 其他客户端修改这个key的值 |
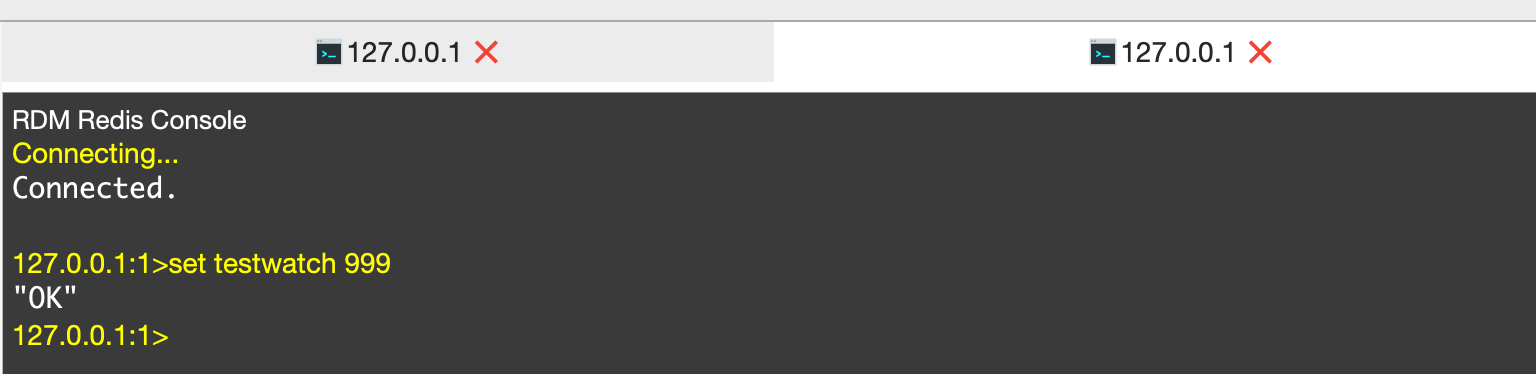
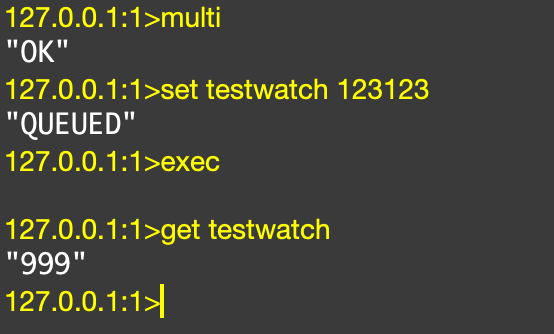
A客户端在事务中尝试修改该Key的值
1 | 127.0.0.1:1>multi |
Pipeline和事务的区别
pipeline
pipeline管道:可以一次性打包多条命令,通过管道一次性发送,发送成后一次性读取服务器执行返回的响应,只消耗了一次网络开销。
优点:
- 降低了传输多条命令的网络开销和连接redis服务器的开销。
- 通过管道一次性发送的命令,如果数据量较少,命令可以存储在内存缓冲区,redis可以保证这些缓冲区的命令的原子性
- 如果命令太多,需要分批发送的话,就无法保证 原子性。
- 可以提服务器的吞吐能力,并提高Redis处理查询请求的能力。
开启事务是在服务器上操作的,而Pipeline是 客户端上操作的。
事务
开启事务后,客户端一条命令一条命令发送给redis,redis收到后存入缓存队列中,等待收到exec执行命令后 开始执行命令。
优点:
没有优点,简直low爆了,反正不建议使用redis的事务
缺点:
- 发生了错误事务无法回滚
Redis 7.0新特性
Redis7.0进行了重大的性能优化,性能优化包括降低写入时复制内存的开销、提升内存效率,改进 fsync 来避免大量的磁盘写入和优化延迟表现。
Redis 主从复制原理
redis的主从复制主要有2个情况:
- 全量复制
- master节点fork 子进程产生内存快照序列化成RDB文件同步到从库,从库RDB文件的数据到本地内存
- 增量复制
- 在master生成RDB快照的过程中,如果有新的操作命令,会存入到 master的内存缓存 - 复制积压区(ReplicationBacklog),等master与slave完成同步后,主库会把积压区的命令发送给slave 进行同步
Redis 主从复制缓存产生的问题
多从库时主库内存占用过多
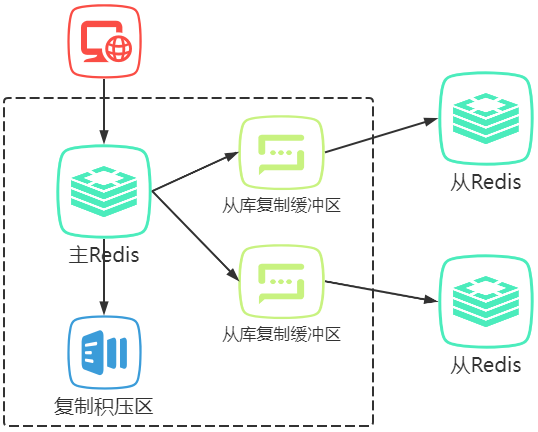
从库复制缓冲区(OutputBuffer)
当slave节点连接到master节点后,master会为每个slave节点 在本地内存中创建一个 从库复制缓冲区
当slave节点断开连接后,master会在内存中删除该缓冲区
复制积压区(ReplicationBacklog)
- 存储 master生成RDB快照期间的新增操作命令
- 存储 master收到的客户端的操作命令
当master收到客户端的操作命令,会将命令存入到 从库复制缓冲区和复制积压区。全量同步时依然会执行该逻辑,所以在全量同步阶段经常会导致 从库复制缓冲区溢出( client-output-buffer-limit),导致master断开与slave的连接,导致主从同步失败,甚至出现循环持续失败的情况。
内存占用过多
master会为每个slave创建一个从库复制缓冲区,假设 client-output-buffer-limit是1GB,如果有5个slave,就会占用5个GB,非常占用内存资源,且生产环境中 slave节点是都是不确定的,基本上都是会弹性调整,内存消耗更加不可控。
OutputBuffer 拷贝和释放的堵塞问题
Redis 为了提升多从库全量复制的效率和减少 fork 产生 RDB 的次数,会尽可能的让多个从库共用一个 RDB,从代码(replication.c)上看:
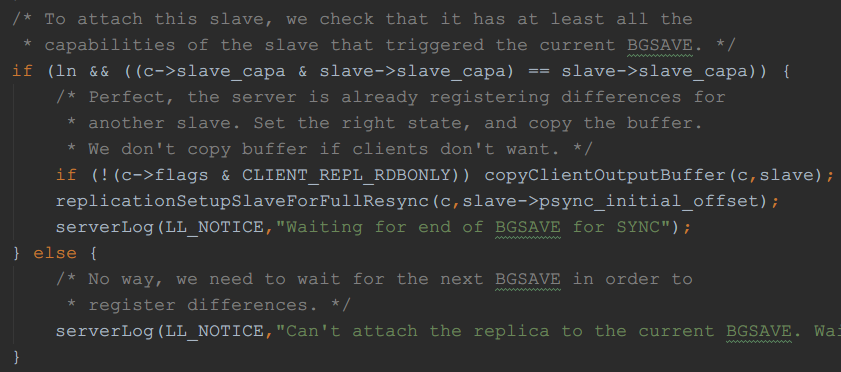
当master出发了RDB BGSAVE后,会生成RDB快照,后续如果有其他的slave需要全量同步的话,会共享这个RDB快照,master会把RDB的数据拷贝到 需要同步的slave的从库复制缓冲区(OutputBuffer)。
问题一:
由于OutputBuffer的数据可能有几百M甚至几个G,拷贝OutputBuffer是非常耗费性能的事情,对其拷贝可能使用百毫秒甚至秒级的时间,可能存在 主线程堵塞的情况,一旦主线程堵塞了,堵塞期间无法对外提供服务。
问题二:
当 OutputBuffer 大小触发 limit 限制时,Redis 就是关闭该从库链接,而在释放 OutputBuffer 时,也需要释放数百 MB 甚至数 GB 的数据,其耗时对 Redis 而言也很长。
ReplicationBacklog 的限制
client发送新的操作命令给master后,master会写入到复制积压缓冲区(ReplicationBacklog)和OutputBuffer(从库复制缓冲区)。
slave断线后,master会清空对应的从库缓冲区,当slave再次连上master,会根据slave最后一条同步的记录去ReplicationBacklog中寻找,如果能找到的话就会进行增量同步。
如果开始增量同步后,则主库会从 ReplicationBacklog 中拷贝从库缺失的数据到其 OutputBuffer,拷贝的数据量最大当然是 ReplicationBacklog 的大小,为了避免拷贝数据过多的问题,通常不会让该值过大,一般百兆左右。
但在大容量实例中,为了避免由于主从网络中断导致的全量同步,又希望该值大一些,这就存在矛盾了。
redis运行期间调整 复制积压区缓冲区大小会有2个问题
- 设置ReplicationBacklog大小,需要重新在内存中开辟一段新的内存空间后,把旧的内存迁移到新的内存中,很耗费时间和性能。
- 如果重新设置 ReplicationBacklog 大小时,会导致 ReplicationBacklog 中的内容全部清空,所以如果在变更该配置期间发生主从断链重连,则很有可能导致全量同步。
主从复制的数据结构
Trie树
Trie又称字典树、前缀树,是一种树形结构。广泛应用于统计和排序大量的字符串(但不仅限于字符串),所以经常被搜索引擎系统用于文本词频统计。它的优点是最大限度地减少无谓的字符串比较,查询效率比较高。
Trie的核心思想是空间换时间,把字符串的前缀相同提取出来,存入Trie树中,下次查询的时候,可以通过字符串的前缀来查询,可以有效降低查询的时间,提高查询效率。
举个例子:
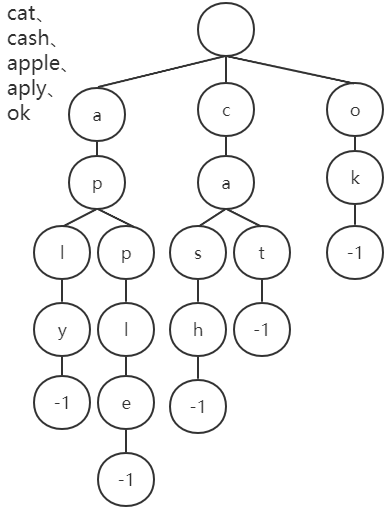
字符串:cat 、cash 、 apple 、aply 、ok
问题一:如果我们把以上几个字符串存储到某个数据结构中,当我们需要判断某个字符串是否存储过,可以用什么来实现?
答案:可以使用Map来实现,直接使用 字符串作为key名称就行
问题二:如果我们需要判断 某个字符串的前缀,在几个字符串中出现过,如何实现?
答案:通过Map也可以实现,不过复杂度会非常高,为此就可以考虑更加高效的数据结构,如:Trie树来实现
插入数据
- 当我们插入一个新的字符串时候,会把字符串拆分成每个单词,并按顺序依次的存入Trie树中。
从Trie树结构图中可以看出:
每一个节点代表一个字符
有相同前缀的单词在树中就有公共的前缀节点。
整棵树的根节点是空的,每个节点结束的时候用一个特殊的标记来表示,这里我们用-1来表示结束,从根节点到-1所经过的所有的节点对应一个英文单词。
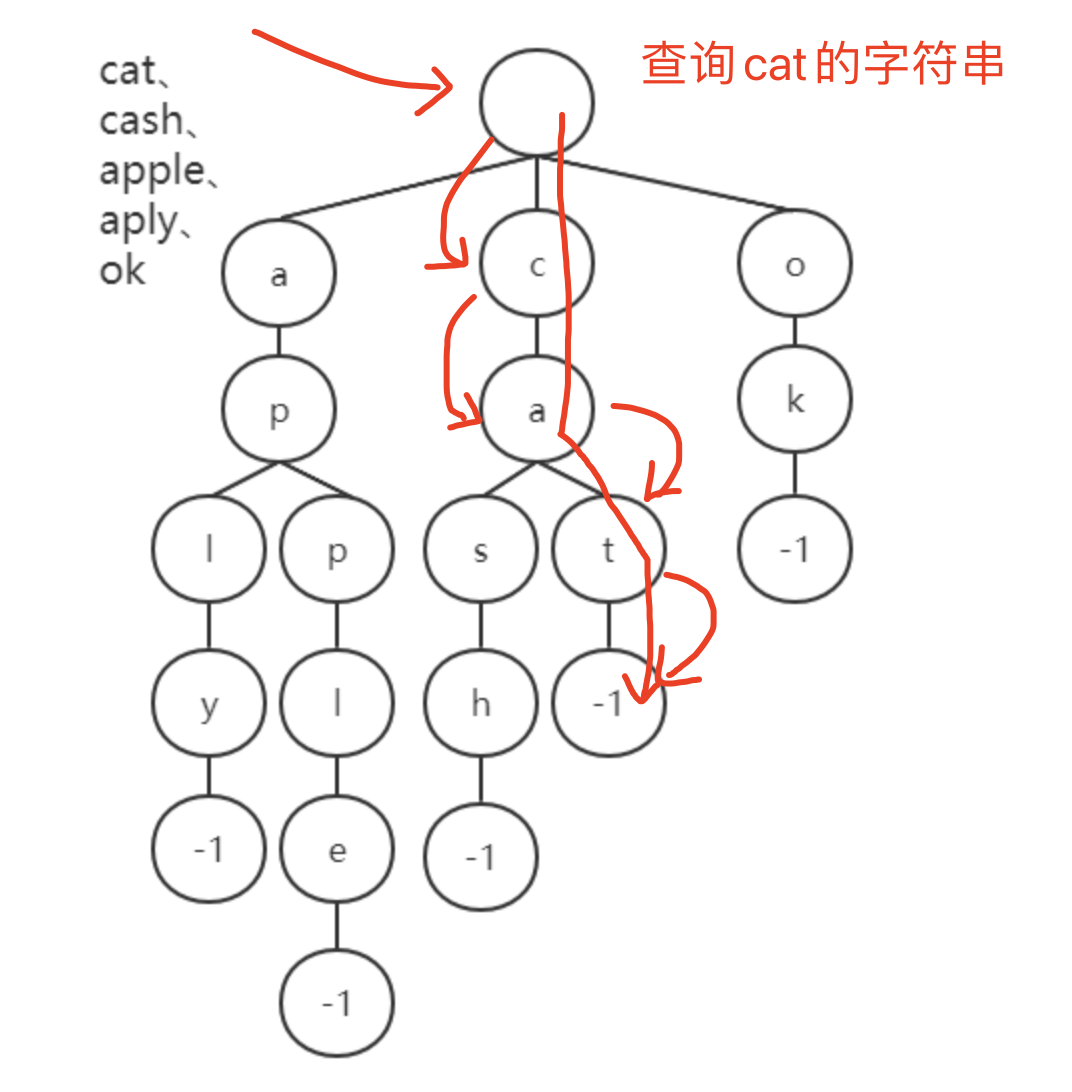
查询和插入的时间复杂度为O(k),k为字符串长度,当然如果大量字符串没有共同前缀时还是很耗内存的。
rie树把很多的公共前缀独立出来共享了。这样避免了很多重复的存储。想想字典集的方式,一个个的key被单独的存储,即使他们都有公共的前缀也要单独存储。相比字典集的方式,Trie树显然节省更多的空间。
如果大量的字符串没有共同的前缀时,Trie树是比较浪费空间。
比如这个字符串列表:”deck”, “did”, “doe”, “dog”, “doge” , “dogs”。”deck”这一个分支,有没有必要一直往下来拆分吗?还是”did”,存在着一样的问题。像这样的不可分叉的单支分支,其实完全可以合并,也就是压缩。
Radix树:压缩后的Trie树
所以Radix树就是压缩后的Trie树,因此也叫压缩Trie树。比如上面的字符串列表完全可以这样存储:
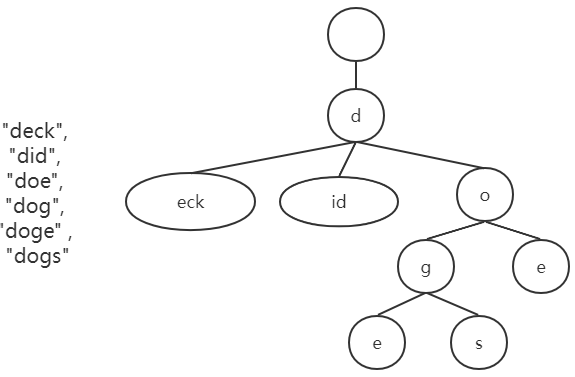
同时在具体存储上,Radix树的处理是以bit(或二进制数字)来读取的。一次被对比r个bit。
比如”dog”, “doge” , “dogs”,按照人类可读的形式,dog是dogs和doge的子串。
但是如果按照计算机的二进制比对:
dog: 01100100 01101111 01100111
doge: 01100100 01101111 01100111 01100101
dogs: 01100100 01101111 01100111 01110011
可以发现dog和doge是在第二十五位的时候不一样的。dogs和doge是在第二十八位不一样的,按照位的比对的结果,doge是dogs二进制子串,这样在存储时可以进一步压缩空间。




